デザインの幾何学的観察―東京五輪エンブレム「組市松紋」【Tweetまとめ＋】

2016/04/30

♪ガラガラ
I’M IN LOVE WITH 幾何学的な ガラガラ

こんにちは、Cibo Mattoです。ウソです。

細かすぎて伝わらない「デザインあ」のコーナーギャグから入ってみました。

さて、4つの候補作から五輪エンブレムに選ばれた「組市松紋」については、公表後Twitter上で優れた解析報告がいくつもされています。こと本件に関しては、他メディアはテレビもネットもみんな後追いです。

とはいえ、個々の発見事実は素晴らしいながらもいずれも断片的で、いまだ「組市松紋」の全貌が把握できていない感があります。そこでひとまず現段階での状況整理を目指し、頼まれもしないのにデザイン芸人が主なツイートに周辺情報を加えてまとめておくことにいたしました。

ここでは「寡黙」な解析対象にあやかり、なるべく余計な説明を加えずに並べていく方針とします。

要約：Executive Summary

東京2020オリンピック・パラリンピック競技大会エンブレムに決まった「組市松紋」を読み解くキーワードは、「3の倍数」です。

どこへ進んでも3の倍数づくしで、アホが止まらなくなるほどです。

デザインの観察：組市松紋

Web

東京2020大会エンブレム｜tokyo2020.jp より

デザインの観察
Cornelius
￥250

第一印象

基本構成

図を見てわかりました。3種類の四角形はこうやって作っているんですね。

2016-04-30_1356

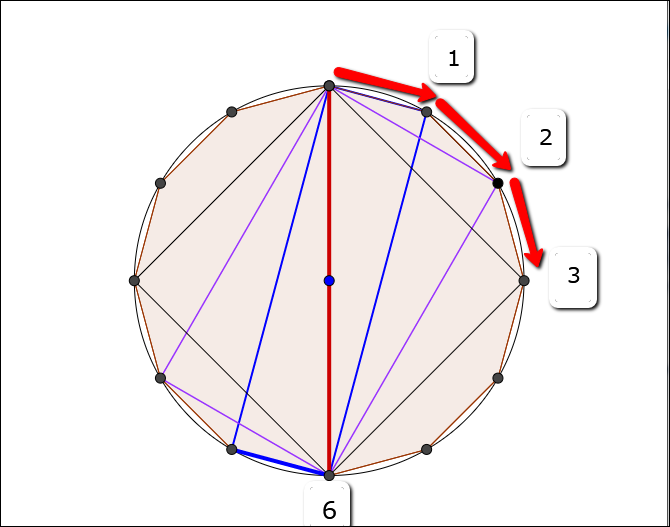
構成パーツとなるこれらの四角形を順に

  • 四角形１（小）
  • 四角形２（中）
  • 四角形３（大）

と名づけておきます。

補足：理解の助けとして

あるいは「日常的に見慣れた12角形」のこいつをイメージすれば、理解しやすくなるかもしれません。

20160428_clock-1141545_640

要するに、

    • 3つの四角形各々の頂点は、
  • 四角形１（小）＝1, 6, 7, 12時
  • 四角形２（中）＝2, 6, 8, 12時
  • 四角形３（大）＝3, 6, 9, 12時

の位置にある。という話です。

そして3つの四角形には、こういう性質があります。

  • 対角線が共通
  • 四角形の対角線で区切られる三角形の、二辺の長さもすべて共通
  • 短辺に外接する円弧（または正12角形の一辺）の比が1：2：3

24角形であって、「正」でないのがミソ

ちょっと細かい話。

外周部の24角形は「正」24角形ではありません。部分部分で一辺の長さが微妙に違います。こちらのツイートで指摘されていました。

以上の事実から予想できるのは、「24角形」はこの図形の本質ではないということです。

「3回の回転対称」（オリンピック）

HIRANO KEIKO’S OFFICIAL BLOG ＞032 1対3の構図 – 「A案」VS「BCD案」より：

（4月9日版）※下線は引用者

（2）基本形状
「A案」は、正円。オリンピック・エンブレムは、パーツの市松の配置に一部非対称性はあるものの、印象としてはシンメトリー。（後略）

正円？

厳密には正円じゃなくてそれに近い多角形なんだけど、まあいっか。

それより「配置に一部非対称性はある」だって？

【事例】120度（3回）回転対称の家紋たち

オリンピックエンブレムの「円相」と同じような120度の回転対称になった家紋を見つけ出すことは、さほど難しくありません。ハリウッド―モン・トコロ―ガラシショウ（野老朝雄さんを勝手にそう呼んでみた）がここらをイメージしてオリンピックの組市松紋をハンマーカンマーしたかは不明ですけれども、数点ピックアップしておきます。

以下、Amazonで売っていた家紋マウスパッドより


〈三つ扇〉


〈三つ橘〉


〈丸に剣片喰〉

ですわね。

みんないまにも回りだしそう。とってもクールでダイナミック ！

ちなみに最後のは父方の家紋。だから剣片喰は「けんかたばみ」と読むのを知ってる。わりとどうでもいい。

下は、同じく032 1対3の構図 – 「A案」VS「BCD案」 から。

（3）造形モティーフ
「A案」は、市松という伝統的な文様を引用した抽象表現。静的な印象。

パラリンピック側はおいて、回転対称のシンメトリー図形が「静的な印象」なのか。言っちゃ悪いが平野敬子さん、どうかしてるぜ。

（4月12日修正版）

（2）基本形状
「A案」は、正円。オリンピック・エンブレムは左右対称形ではないものの、左右対称形のような印象に見える。（後略）

文章を再考し、修正した文章を4月12日に更新しましたことを報告いたします。間違いをご指摘下さいましたみなさまへ、感謝申し上げます。

間違いを認めて改められる人、好きです。Nobody’s perfect.

何から何まで「同じ」

たくさんシェアされている上のツイートのGIFよりも、こちら↓のエンドレス版アニメがより楽しいです。

そして「なんでそんなことができるの？」の秘密は、隠されたグリッド構造にありそうです。この件は後ほどまた。

（2016/05/02追記）
こちらでの説明がすこぶるエレガントでした。

「基礎編」決定版が出た感があります。

組んでみた

以上をふまえ、カラーペーパーを切って実際に床の上に並べてみました。楽しい。

わーい。なんかほめてもらった。

これもありがたいことです。

「つくってみよう！」の野望

単なる興味から手を付けましたが、途中から「これ、小学生向けのワークショップ教材として使えるなあ」と「授業計画」を練りながら組んでいました。

文部科学省の学習指導要領によると、いま「多角形」「正多角形」は5年生の算数で学ぶらしいです。それらを習った次の授業時間あたり狙って「つくってみよう！」を開けば盛り上がると思うけど、どうだろう。

いずれにしても、ここのつづきは記事をあらためて。

「表彰台」説

配色を変えると、また違ったイメージが喚起されます。こちらもその一例かも。

素敵な見立てです。

この伝でいくと、15×3で構成される五輪の円相は、表彰台（Podium）になるようにパーツ15個の単位を区切るのがきっと「正解」ですね。

そうしてみると、見慣れたアイコンそのままの「Google Chrome分割」（下に再掲）も、表彰台がきれいにできがりますので、あながち間違っていない気がします。

面積

補足

以下、計算されてからの後出しジャンケン結果論だけれど、補完します。

くり返すと、パーツとなる四角形１（小）、２（中）３（大）は

  • どれも対角線が共通
  • つまり、対角線で区切られる三角形の二辺の長さも共通
  • 短辺に外接する円弧（または正12角形の一辺）の比が1：2：3

である。

さらに加えて、

2016-04-30_1303

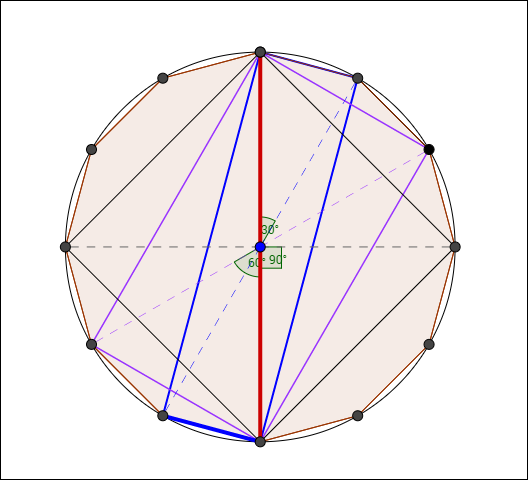
対角線の交差角の組み合わせがそれぞれ、

  • １（30°, 150°）
  • ２（60°, 120°）
  • ３（90°, 90°）

となっている。

なのでその面積の比もそのまま
sin30°：sin60°：sin90° に比例するから、

＝1/2：√3/2：1
（各項を2倍して）
＝1：√3：2 となる。

まあ当然っちゃ当然の帰結です。

正弦定理を用いれば求められる、のかな？ 正直よくわかってない。三角関数ムズい。

ちなみに、上図の正12角形やら対角線やらのもろもろは、ブラウザからGEOGEBRAにアクセスして描きました。

「ひし形タイリング」説の発見

「なんで角度を一切変えずに組み替えられるの？」の秘密は、どうもこのあたりにありそうです。

なんだかすんごいものができあがっているぞ！

ほとんど独走の解析

見つけられた範囲で言えば、以下のやり取りは間違いなく「組市松紋」解析の先頭集団に属しています。

幾何学的観点でエンブレムに興味を持っている諸氏も、いまだ大半はこの水準にまで至っていないように思われますので、ほとんど独走状態です。

ひし形タイリングで遊ぼう！

どんどん考察が進んでしまっていました。正直ついていけてません。

あくまで感覚値でのもの言いですが、橋本環奈さんにも匹敵する1000人に1人レベルの先進性を感じます。

快感です。

まとめのまとめ：3の倍数づくし

まとめを再度まとめます。「組市松紋」で3の倍数が出てくる特徴を列挙します。

世界のナベアツさんみたいに、3の倍数や3のつく数字だけアホになってみるのも一興です。

＜オリンピック・パラリンピック共通＞

  • 3種類の四角形で構成
  • パーツは全部で45個
  • その内訳は、面積の小さい方から18・18・9個
  • どれも正12角形の対角線（もしくは一辺）が基準
  • 四角形の2本の対角線の交差角（狭い方）は、順に30°、60°、90°
  • それぞれ、外接円の12分割・6分割・4分割に対応

オリンピックの「円相」

  • 120度回転対称
  • パーツ配置は（6＋6＋3）＝15×3個

この区切り方が、けっこう好き（気に入ってるので再々掲）。

パラリンピックの「鶴」

  • 線対称
  • パーツ配置は、片側（8＋9＋4）＝21×2＋正中線上に3（2＋0＋1）個

こっちもわりと三づくし

さて、3の倍数でアホになったり5の倍数で犬っぽくなったりして一世を風靡した世界のナベアツさんですが、2011年に当時の桂三枝（現・桂文枝）さんに弟子入りしてからは「桂三度」の芸名で活動されています。

2016-04-30_2046

桂三度｜天満天神繁昌亭 上方落語家名鑑 より

でもって、上方落語で桂文枝一門の紋といったら、「三つ柏」と「結び柏」です。

画像検索した印象では、「簡略表現」である結び柏が多用されているようです。

20160430_240px-Musubi-kashiwa

musubi-kashiwa from commons.wikimedia.org

結び柏

三つ柏を簡略表現した紋です｡文枝一門と米朝一門は三つ柏か結び柏を用い､春團治一門は別の紋を使っています｡

出典：文枝にまつわる家紋｜yoshimoto.co.jp

文枝さんも、羽織の紋が結び柏です。

※画像は、神保町花月 ～桂文枝プロデュース～ 戀する落語会 パートⅠ 『三度は3度“笑ぶ”する』｜よしもとニュースセンター（2014/06/17付）より

桂三度さんのブログ「桂三度の坂壱」を見てみると、なんとびっくり！

20160430_custom_header

ヘッダー画像が市松模様になっていました。

めちゃめちゃよくできた話です。

本調子中の舞
林家染丸社中
￥150

隣のエンブレムに正12角形の囲いができたで。
へぇ～！

組市松紋の一席、お時間でございます。

スポンサーリンク

コメント

タイトルとURLをコピーしました